
In other words, $3 \cdot 27 = 1 + 40k$ for some (positive, in fact) integer $k$. The relationship between 27 and 3, which made things work, is that We found the exponent 27 - reversing the cubing operation - by an ad hoc sort of procedure.
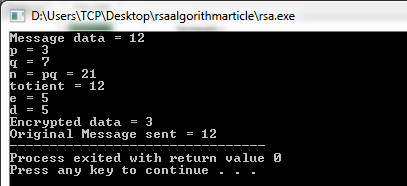
This will happen in some False lines too, but not reliably since Euler's theorem does not apply there. In every line ending with True, the first and third numbers should match. ''' def f ( n ): D = decompose ( n ) result = 1 for p in D : result = result * f_pp ( p, D ) return result return f return decomp def mult_function ( f_pp ): ''' When a function f_pp(p,e) of two arguments is input, this outputs a multiplicative function obtained from f_pp via prime decomposition. current_number = current_number // p # Factor out p. decomp = 1 # Creates a new entry in the dictionary, with key p and value 1. else : # "else" here means "if p is not in decomp.keys()". keys (): # Is p already in the list of keys? decomp = decomp + 1 # Increase the exponent (value with key p) by 1. ''' if n 1 : p = smallest_factor ( current_number ) # The smallest prime factor of the current number. def smallest_factor ( n ): ''' Gives the smallest prime factor of n.

The material in this notebook complements Chapter 7 of An Illustrated Theory of Numbers.įrom math import sqrt # We'll want to use the square root. Computationally based on modular exponentiation, its security rests on the difficulty of factoring large numbers.
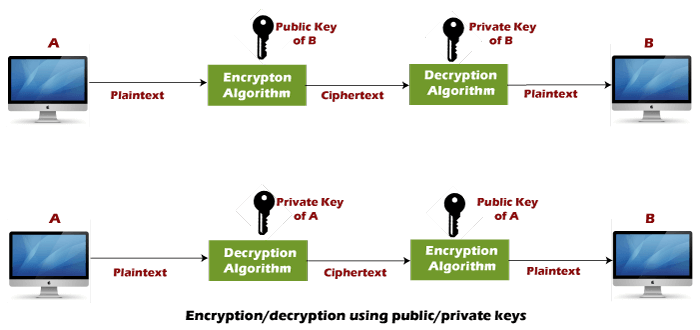
For such a purpose, we introduce the RSA cryptosystem. We need something asymmetric - something one person can do that no other person can do, like a verifiable signature, so that we can be sure we're communicating with the intended person. To thwart such an attack, we need some type of authentication. In this way, Alice and Bob think they are talking to each other, but Eve is just passing (and understanding) their messages the whole time! She goes through the Diffie-Hellman protocol with each, obtaining two secret keys, and decrypting/encrypting messages as they pass through her computer. To Alice, she pretends to be Bob, and to Bob, she pretends to be Alice. For example, imagine a "man-in-the-middle attack": Alice and Bob wish to communicate securely, and begin the Diffie-Hellman protocol over an insecure line. In order for two parties to share the same secret key, we studied the Diffie-Hellman protocol, whose security rests on the difficulty of the discrete logarithm problem.Īlthough this represents progress towards secure communication, it is particularly vulnerable to problems of authentication. The same key is used for both encryption and decryption, so we say it is a symmetric key cipher. The Vigenère cipher we studied uses a secret key for encrypting and decrypting messages. In the previous notebook, we studied a few basic ciphers together with Diffie-Hellman key exchange.


 0 kommentar(er)
0 kommentar(er)
